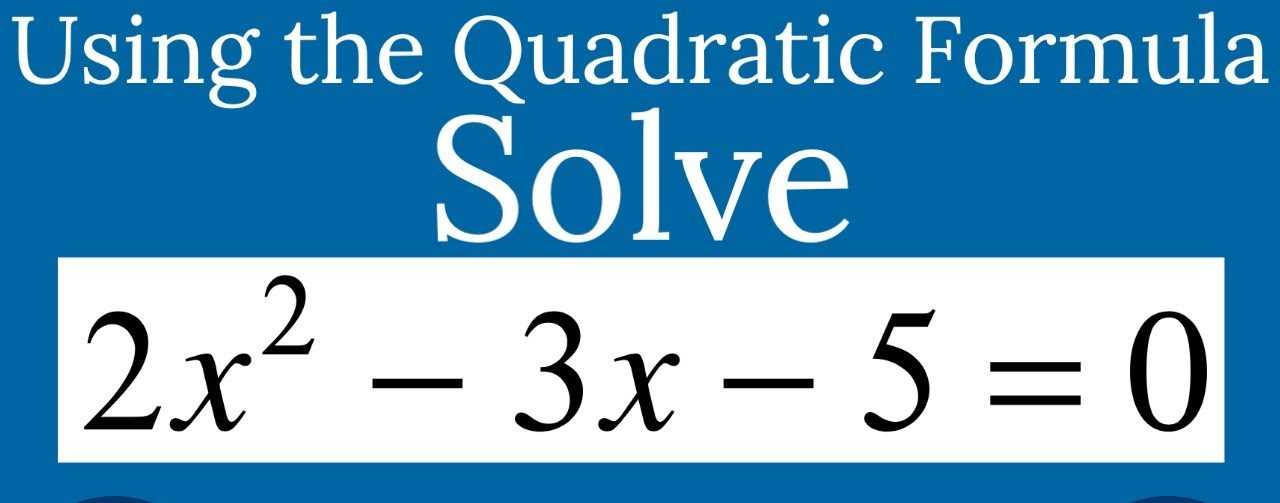2×2-3x- 5 = 0: Solved

In this comprehensive exposition, we embark on a deep and enlightening exploration of the equation 2×2-3x- 5 = 0. Within the captivating realm of mathematics, equations emerge as the bedrock upon which the entire structure of problem-solving is constructed. They serve as the conduits through which we gain profound insights into the intricate interplay of variables and, more importantly, unearth the solutions to real-world conundrums. This journey will encompass not only the unraveling of its roots but also a meticulous examination of multiple methodologies for solving it. Additionally, we shall shine a spotlight on its nuanced significance within a plethora of mathematical and practical contexts.

The Quadratic Equation 2×2-3x- 5 = 0

What is a Quadratic Equation?

At the heart of our mathematical odyssey lies the quadratic equation, a polynomial equation of the second degree. Its paramount importance lies in the fact that it boasts the highest power of 2 within its structural makeup. To delve further into this realm, it is imperative to acquaint ourselves with its general form:

Ax² + Bx + C = 0

In the specific context of our equation, 2×2-3x- 5 = 0, we can discern the following constants: A = 2, B = -3, and C = -5. Now, let us embark on a profound journey to unearth the intricacies concealed within this mathematical masterpiece.

Finding the Roots of 2×2-3x- 5 = 0

The primary and pivotal objective when grappling with a quadratic equation is the identification of its roots, often referred to as solutions or zeroes. These elusive values of ‘x’ are the proverbial keys that unlock the door to making the equation a true statement. Our quest now begins to uncover these enigmatic roots, the very essence of our equation’s existence.

Methods for Solving 2x² – 3x – 5 = 0

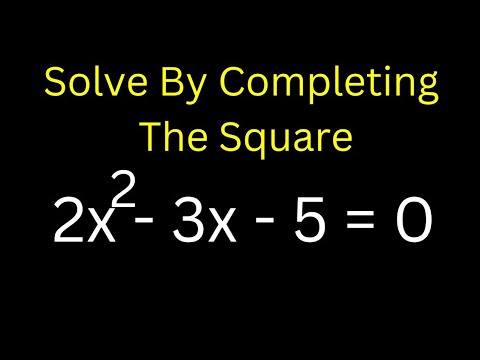
Method 1: Factoring

One of the classic techniques for solving quadratic equations is the method of factoring. However, as mathematics often reveals, the path to solutions is not always straightforward. In the case of our equation, 2×2-3x- 5 = 0, it does not readily yield to simple binomial factoring. This enigma beckons us to explore alternative approaches that will unlock its secrets.

Method 2: Quadratic Formula

The quintessential and universally embraced method for resolving any quadratic equation is the venerable quadratic formula. This formula, often hailed as the magnum opus of mathematical elegance, takes the following form:

x = (-B ± √(B² – 4AC)) / (2A)

With bated breath, we shall now apply this formula with meticulous precision to our equation. Armed with the knowledge that A = 2, B = -3, and C = -5, we embark on a journey that promises to unveil the hidden treasures within:

x = (3 ± √((-3)² – 4(2)(-5))) / (2(2))

This seemingly complex equation is the gateway to the two elusive values of ‘x’ that constitute the roots of 2×2-3x- 5 = 0. The utilization of this formula epitomizes the elegance of mathematics in the art of problem-solving, a testament to human intellect.

Significance and Applications

Quadratic equations are not mere mathematical abstractions; they transcend the confines of theory to manifest their significance across diverse fields. Their pervasive influence stretches across the tapestry of human knowledge and practical applications. Let’s explore how these equations permeate through various domains, both within and beyond the realm of mathematics.

Conclusion

In the world of mathematics, equations like 2×2-3x- 5 = 0 represent the very essence of problem-solving. They embody the spirit of exploration and discovery that fuels our intellectual pursuits. By delving into the methods to solve such equations, we not only unlock the doors to theoretical understanding but also equip ourselves to tackle an array of real-world challenges. Whether you are a student embarking on the journey of algebraic exploration or an enthusiastic aficionado marveling at the beauty of mathematics, a solid grasp of the concepts surrounding quadratic equations is a pivotal step in your intellectual voyage.